 Problem Setting
Problem Setting
We focus on the commonly used synchronous Gradient Descent paradigm for large-scale distributed learning, for which there has been a growing interest to develop efficient and robust gradient aggregation strategies that overcome two key system bottlenecks: communication bandwidth and stragglers' delays. In particular, Ring-AllReduce (RAR) design has been proposed to avoid bandwidth bottleneck at any particular node by allowing each worker to only communicate with its neighbors that are arranged in a logical ring. On the other hand, Gradient Coding (GC) has been recently proposed to mitigate stragglers in a master-worker topology by allowing carefully designed redundant allocation of the data set to the workers. We propose a joint communication topology design and data set allocation strategy, named CodedReduce (CR), that combines the best of both RAR and GC. That is, it parallelizes the communications over a tree topology leading to efficient bandwidth utilization, and carefully designs a redundant data set allocation and coding strategy at the nodes to make the proposed gradient aggregation scheme robust to stragglers. In particular, we quantify the communication parallelization gain and resiliency of the proposed CR scheme, and prove its optimality when the communication topology is a regular tree. Moreover, we characterize the expected run-time of CR and show order-wise speedups compared to the benchmark schemes. Finally, we empirically evaluate the performance of our proposed CR design over Amazon EC2 and demonstrate that it achieves speedups of up to 27.2x and 7.0x, respectively over the benchmarks GC and RAR.
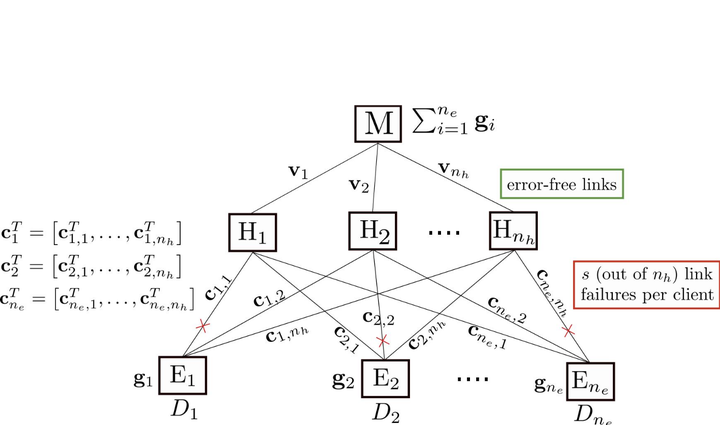
Client devices at the edge are generating increasingly large amounts of rich data suitable for learning powerful statistical models. However, privacy concerns and heavy communication load make it infeasible to move the client data to a centralized location for training. In many distributed learning setups, client nodes carry out gradient computations on their local data while the central master server receives the local gradients and aggregates them to take the global model update step. To guarantee robustness against straggling communication links, we consider a hierarchical setup with $n_e$ clients and $n_h$ reliable helper nodes that are available to aid in gradient aggregation at the master. To achieve resiliency against straggling client-to-helpers links, we propose two approaches leveraging coded redundancy. First is the Aligned Repetition Coding (ARC) that repeats gradient components on the helper links, allowing significant partial aggregations at the helpers, resulting in a helpers-to-master communication load ($C_{HM}$) of $\mathcal{O}(n_h)$. ARC however results in a client-to-helpers communication load ($C_{EH}$) of $\Theta(n_h)$, which is prohibitive for client nodes due to limited and costly bandwidth. We thus propose Aligned Minimum Distance Separable Coding (AMC) that achieves optimal $C_{EH}$ of $\Theta(1)$ for a given resiliency threshold by using MDS code over the gradient components, while achieving a $C_{HM}$ of $\mathcal{O}(n_e)$.