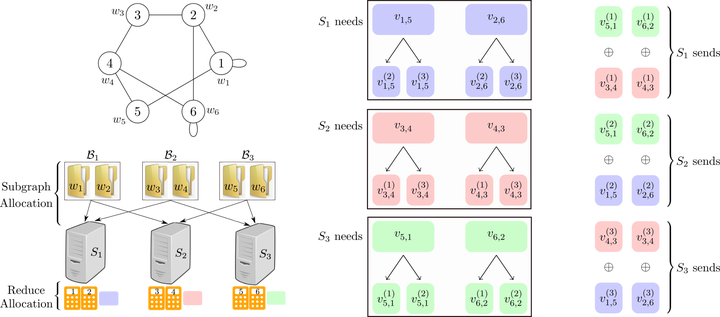
 Scheme Illustration
Scheme Illustration
Many distributed computing systems have been developed recently for implementing graph based algorithms such as PageRank over large-scale graph-structured datasets such as social networks. Performance of these systems significantly suffers from communication bottleneck as a large number of messages are exchanged among servers at each step of the computation. Motivated by graph based MapReduce, we propose a coded computing framework that leverages computation redundancy to alleviate the communication bottleneck in distributed graph processing. As a key contribution of this work, we develop a novel coding scheme that systematically injects structured redundancy in the computation phase to enable coded multicasting opportunities during message exchange between servers, reducing the communication load substantially in large-scale graph processing. For theoretical analysis, we consider random graph models, and focus on schemes in which subgraph allocation and Reduce allocation are only dependent on vertex ID while the Shuffle design varies with graph connectivity. Specifically, we prove that our proposed scheme enables an (asymptotically) inverse-linear trade-off between computation load and average communication load for two popular random graph models - Erdös-Rényi model, and power law model. Particularly, for a given computation load r, (i.e. when each graph vertex is carefully stored at r servers), the proposed scheme slashes the average communication load by (nearly) a multiplicative factor of r. Furthermore, for the Erdös-Rényi model, we prove that our proposed scheme is optimal asymptotically as the graph size increases by providing an information-theoretic converse.
To illustrate the benefits of our scheme in practice, we implement PageRank over Amazon EC2, using artificial as well as real-world datasets, demonstrating gains of up to 50.8% in comparison to the conventional PageRank implementation. Additionally, we specialize our coded scheme and extend our theoretical results to two other random graph models - random bi-partite model, and stochastic block model. Our specialized schemes asymptotically enable inverse-linear trade-offs between computation and communication loads in distributed graph processing for these popular random graph models as well. We complement the achievability results with converse bounds for both of these models.